算法笔记 - BFS

发表于 | 分类于 ，

bg

封面图是我老婆！不接受任何反驳！

简介

​ 广度优先搜索算法（英语：Breadth First Search，缩写为BFS），又译作宽度优先搜索，或横向优先搜索，是一种图形搜索算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

算法流程

​ 从初始节点开始，每次扩展一层节点，并将这些节点存入一个“待扩展队列”，当当前节点遍历完毕后，从“待扩展队列”中取出一个节点，并以它为新的“初始节点”再次扩展。

伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void BFS()
{
	初始节点入队
	标记初始节点
	while(队列不空)
	{
		取出队首节点
		if(当前节点没有被标记并满足题目要求)
		{
			标记当前节点
			把当前节点入队
			······（一些骚操作）
		}
	}
}

如果不太懂，可以看下面的图来感性理解一下。

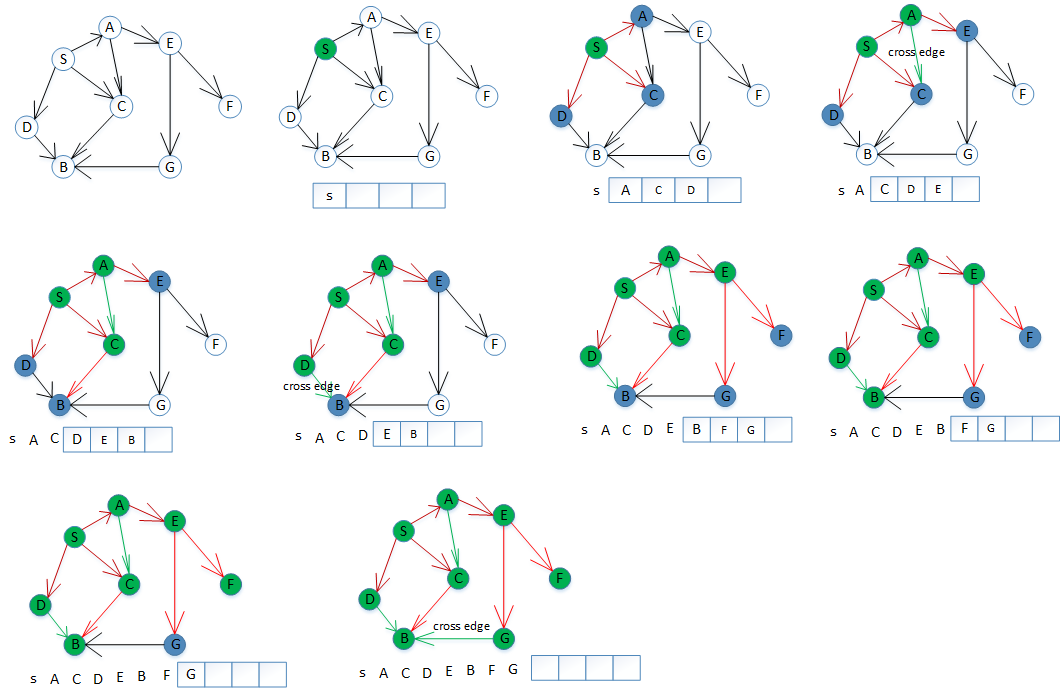
哎呀！图片走丢了！

例题

SYZOJ #73 洪水

题目描述

​ 有一块由$N\ast N（1<=N<=1000）$的小格子组成的土地。有些地方（格子）是山地用$’\ast ‘$表示，有些地方（格子）是平原，用$’.’​$表示。一天最左上角的格子发洪水了（最左上角格子一定是平原）。如果一个格子有洪水，那么它会蔓延至其他4个方向（上下左右）的格子，除非那个格子为山地。问有多少个平原会被淹没。

输入格式

第一行一个整数$N$，表示土地大小

接下来$N$行参见样例

输出格式

一行一个整数，表示有多少个平原会被淹没

样例输入
1
2
3
4
5
6
5
..*..
.*.*.
...**
***..
.....
样例输出
1
7
数据范围与提示

$1\leq N\leq 1000$

思路

​ 这是一道BFS的板子题，以左上角的点为初始节点做一遍BFS，每访问到一个新节点，就让答案加一。在BFS的时候要注意判断要扩展的点是否越界及是否为山地。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<iostream>
#include  <cstdio>
#include   <queue>
#define I_love_Yae_Sakura int main()
#define ri register int
using namespace std;
const int maxn=1010;
int d[4][2]={{0,-1},{0,1},{1,0},{-1,0}};
int n,ans,map[maxn][maxn],vis[maxn][maxn];
struct node
{
	int x,y;
};
void BFS()
{
	queue<node> q;
	q.push(node{1,1});
	vis[1][1]=1;
	while(!q.empty())
	{
		node now=q.front();
		q.pop();
		ans++;
		for(ri i=0;i<4;i++)
		{
			int next_x=now.x+d[i][0],next_y=now.y+d[i][1];
			if(next_x>=1 && next_x<=n && next_y>=1 && next_y<=n && map[next_x][next_y] && !vis[next_x][next_y])
			{
				vis[next_x][next_y]=1;
				q.push(node{next_x,next_y});
			}
		}
	}
}
I_love_Yae_Sakura
{
	ios::sync_with_stdio(false);
	cin>>n;
	for(ri i=1;i<=n;i++)
		for(ri j=1;j<=n;j++)
		{
			char ch;
			cin>>ch;
			if(ch=='.')
				map[i][j]=1;
		}
	BFS();
	cout<<ans<<endl;
	return 0;
}

应用举例

​ BFS是一种非常基础的算法，很多高级算法中也有它的使用，如Dijkstra单源最短路算法和Prim最小生成树算法都用到了和BFS类似的思想。这里介绍一下用BFS求最短路的算法。

用BFS求最短路

​ 如果终点的深度与到达它的“费用”成正比，那么在BFS过程中第一次访问到它时花费的费用就是最优解。符合这种情况的一般是网格图或者边权为$1$的图。

0%