「NOIP2017」列队

发表于 | 分类于 ，

哎呀！图片走丢了！

题目描述

$Sylvia$是一个热爱学习的女孩子。

前段时间，$Sylvia$参加了学校的军训。众所周知，军训的时候需要站方阵。

$Sylvia$ 所在的方阵中有$n\ast m$名学生，方阵的行数为$n$，列数为$m$。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中的学生从$1$到 $n\ast m$编上了号码（参见后面的样例）。即：初始时，第$i$行第$j$列的学生的编号是$(i−1)\ast m+j$。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天中，一共发生了$q$件这样的离队事件。每一次离队事件可以用数对$(x,y)(1\leq x\leq n,1\leq y\leq m)$ 描述，表示第$x$行第$y$列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达这样的两条指令：

1.向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条指令之后，空位在第$x$行第$m$列。

2.向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条指令之后，空位在第$n$行第$m$列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后，下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第$n$行第$m$列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以$Sylvia$想要计算每一次离队事件中，离队的同学的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后方阵中同学的编号可能是乱序的。

输入格式

输入共$q+1$行。

第$1$行包含$3$个用空格分隔的正整数$n,m,q$表示方阵大小是$n$行$m$列，一共发生了$q$次事件。

接下来$q$行按照事件发生顺序描述了$q$件事件。每一行是两个整数$x,y$用一个空格分隔，表示这个离队事件中离队的学生当时排在第$x$行第$y$列。

输出格式

按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学生的编号。

样例输入
1
2
3
4
2 2 3
1 1
2 2
1 2
样例输出
1
2
3
1
1
4
样例解释

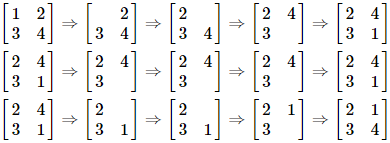
哎呀！图片走丢了！

列队的过程如上图所示，每一行描述了一个事件。

在第一个事件中，编号为$1$的同学离队，这时空位在第一行第一列。接着所有同学向左标齐，这时编号为$2$的同学向左移动一步，空位移动到第一行第二列。然后所有同学向上标齐，这时编号为$4$的同学向上一步，这时空位移动到第二行第二列。最后编号为$1$的同学返回填补到空位中。

数据规模

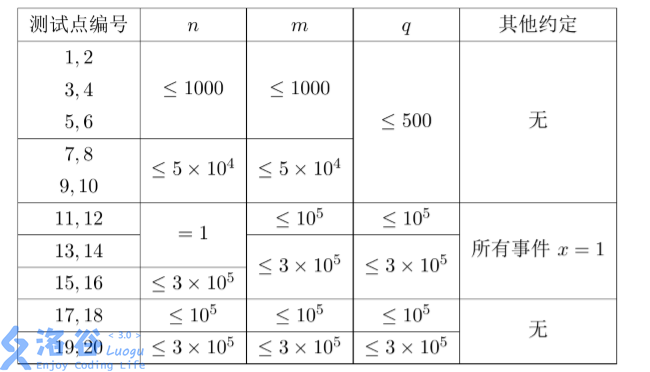
哎呀！图片走丢了！

数据保证每一个事件满足$1\leq x\leq n,1\leq y\leq m$。

思路

把题目抽象一下，我们会发现每一次出队，都会对一些区间产生影响。这就提示我们建立一个可维护的区间，这个区间支持以下两种操作：

  1. 删除第$k$个数。

  2. 在结尾添加一个数。

那么我们如何维护这样一个区间呢？考虑用树状数组来维护，我们用$0$表示某数已删除，用$1$表示某数已插入。当我们插入一个数$s$时，只需执行$change(s,1)$，当我们删除一个数$s$时，只需执行$change(s,-1)$，当我们要查询删除的第$k$个数是多少时，只需要找到哪个位置的前缀和是$k$，这个位置就是这个数。

找到了这个绝妙的方法，我们激♂动的给每一行和最后一列都开了一个树状数组来维护，结果发现内存原地爆炸······怎么办的？进一步观察可以发现，每一次出队，只会对出队人所在的哪一行和最后一列产生影响。所以我们可以借鉴滚动数组的思想，只开一个树状数组，依次维护每一行的前$m-1$个数，处理出每个不在最后一列的操作的出队人的编号在树状数组中的位置。再对最后一列单独处理。

而且对于每一行上从未出队的人，我们可以通过计算得到他们的编号，所以我们只需要用$vector$存下每一行和最后一列后加进来的数。

那么我们最多需要多大的树状数组呢？因为有$q$次询问，所以一行上最多增加$q$个数。所以我们最大需要$max(n,m)+q$的树状数组。空间上是完全可以接受的。

说了这么多，来看看代码吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include<iostream>
#include  <cstdio>
#include  <vector>
#define I_love_Yae_Sakura int main()
#define ri register int
using namespace std;
const int maxn=300010;
struct question
{
    int column,id;
};
long long ans;
int n,m,q_sum,maxx,q[maxn][2],pos[maxn],a[maxn*2];
vector<question> qq[maxn];
vector<long long> num[maxn];
inline int read()
{
    char ch=getchar();
    int x=0,f=1;
    while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
inline int lowbit(int x)
{
    return x&-x;
}
void change(int x,int data)
{
    while(x<=maxx)
    {
        a[x]+=data;
        x+=lowbit(x);
    }
}
int query(int x)
{
    int tot=0;
    while(x>0)
    {
        tot+=a[x];
        x-=lowbit(x);
    }
    return tot;
}
//用二分找位置
inline int find(int x)
{
    int l=1,r=maxx,mid;
    while(l<r)
    {
        mid=(l+r)>>1;
        if(query(mid)<x)
            l=mid+1;
        else
            r=mid;
    }
    return l;
}
I_love_Yae_Sakura
{
    n=read();
    m=read();
    q_sum=read();
    maxx=max(n,m)+q_sum;
    for(ri i=1;i<=q_sum;i++)
    {
        q[i][0]=read();
        q[i][1]=read();
        if(q[i][1]!=m)
            qq[q[i][0]].push_back(question{q[i][1],i});
    }
    for(ri i=1;i<=maxx;i++)
        change(i,1);
    //预处理每一个不在最后一列的操作
    for(ri i=1;i<=n;i++)
    {
        for(ri j=0;j<qq[i].size();j++)
            change(pos[qq[i][j].id]=find(qq[i][j].column),-1);
        for(ri j=0;j<qq[i].size();j++)
            change(pos[qq[i][j].id],1);
    }
    //统计答案
    for(ri i=1;i<=q_sum;i++)
    {
        int x=q[i][0],y=q[i][1],sum;
        change(sum=find(x),-1);
        //如果sum小于n，说明这个数本来就在最后一列，直接算出来
        //sum大于n就是后加进来的数，从vector中提取
        ans=(sum<=n)?(long long)sum*m:num[0][sum-n-1];
        if(y!=m)
        {
            num[x].push_back(ans);
            //与上面同理
            //另：1ll是强制类型转换，将(x-1)*m变成long long类型的
            ans=(pos[i]<m)?(1ll*(x-1)*m+pos[i]):num[x][pos[i]-m];
        }
        num[0].push_back(ans);
        printf("%lld\n",ans);
    }
    return 0;
}
0%